Introduction to Mealy automata, Grigorchuk group and the Burnside problem

26 Jun 2018

Hello! After a quite long pause, semidoc comes back, with the long-awaited post by Thibault Godin about his research. Thibault is currently postdoc in Turku, Finland, but was PhD student when he gave a talk at the PhD seminar. After this post, Victor Lanvin replaces me as “maintainer” of this blog. Enjoy!

---

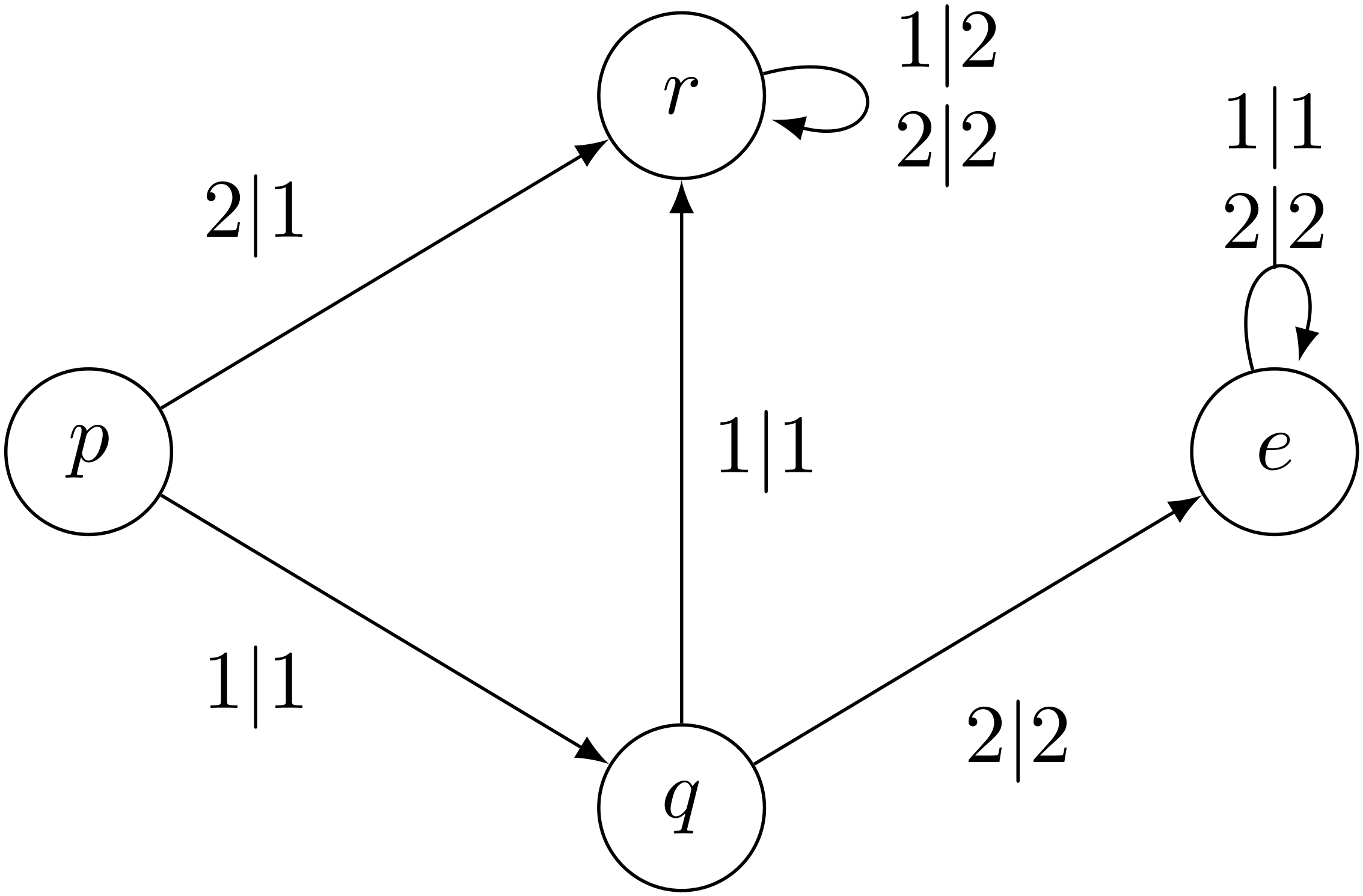
During my PhD, I have been mostly looking at drawings like this one:

The Grigorchuk automaton

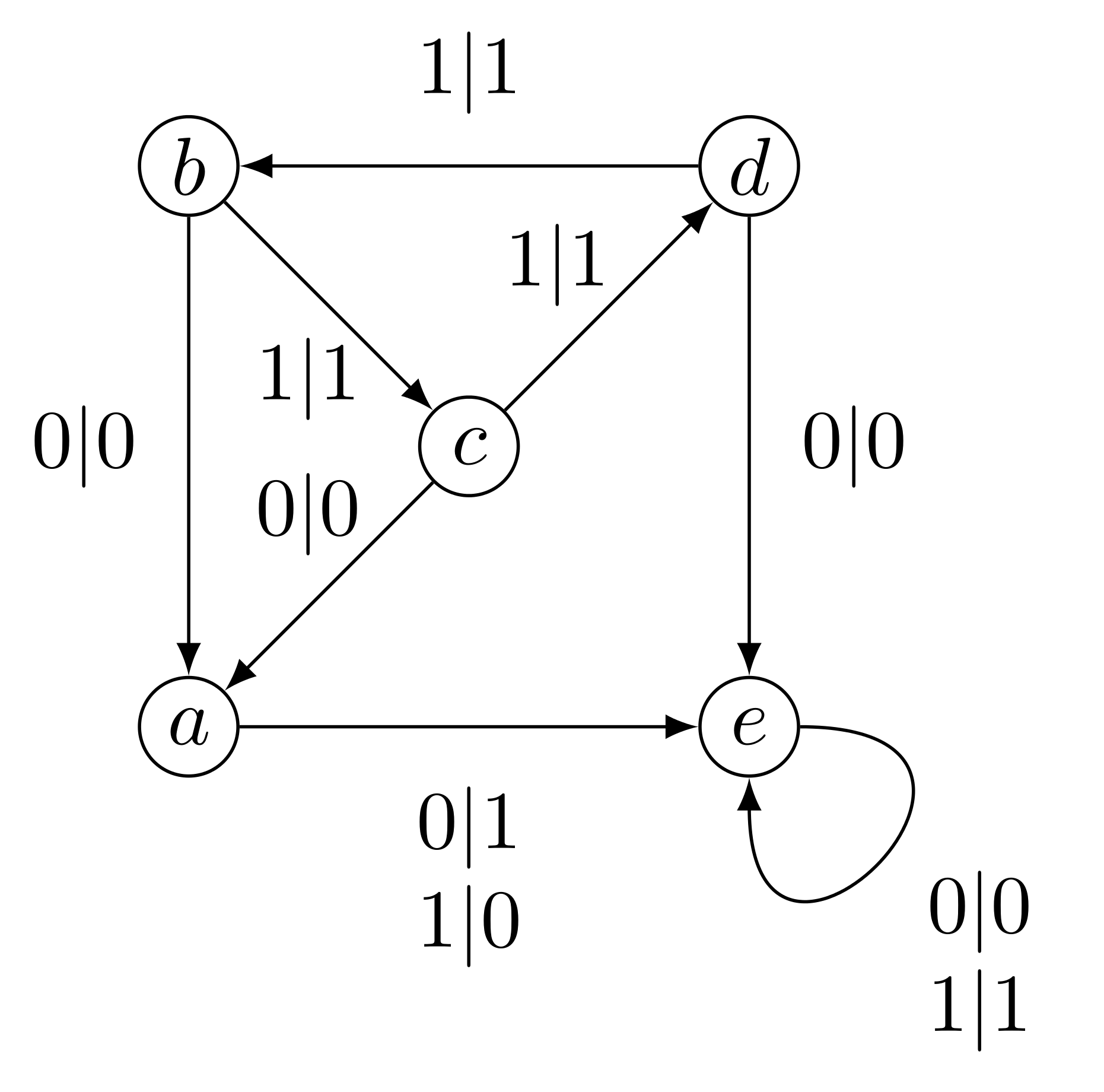
Theses drawings are called Mealy automata, and in this note we will see how they can be used to solve important problems arising from group theory. More precisely we aim to prove that the group generated by the automaton above solves Burnside Problem, i.e. is on the edge between finite and infinite groups. We will first explain how this automaton can represent a group, then why is this group infinite and finally why are every elements of this group of

finite order.

Mealy automata and groups

We see that the graph of the first figure has vertices labelled by letters and edges (called transitions) of the form $x|y$ with $x,y \in \lbrace 0,1 \rbrace$. We are going to call $a,b,c,d,e$ the states of the automaton, $\lbrace 0,1 \rbrace$ its alphabet, $x$ the input letter of the transition, and $y$ the output letter of the transition.

As for a classical automaton, the main move is, from a state, to read a letter. For instance reading $0$ from the state $b$ leads us to $a$ outputting $0$, because the transition is $b \xrightarrow{ 0\mid 0} a $. This action can be easily extended, and from a state we can read a word of letter. For instance if we want to read, from the state $b$, the word $0100$, we start as before by following the transition $b \xrightarrow{ 0\mid 0} a $, outputting $0$. What left to do is to read the word $100$, now from $a$, so we follow the transition $a \xrightarrow{ 1\mid 0} e $, and we iterate this process until there is no more letter to be read. To summarise we have went through the states $b,a,e$ and $e$, outputting $0000$. This can be read as a path in the automaton:

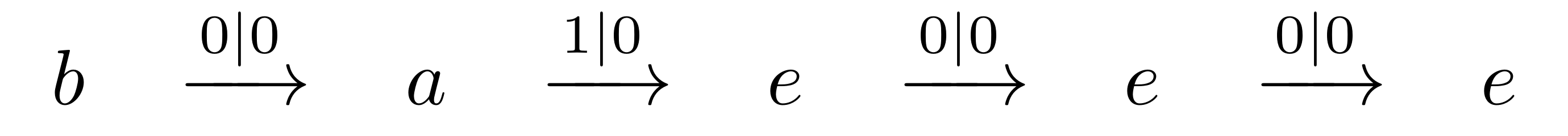
or equivalently

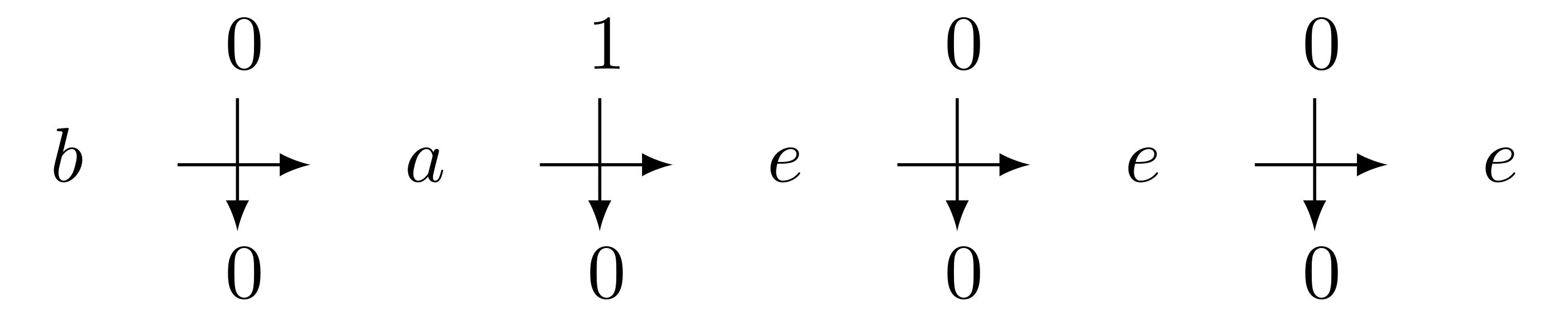
As we see, $b$ transforms $0100$ into $0000$. As we can do this for any word, we can say that $b$ induces a transformation $\rho_b$ from $ \lbrace 0, 1 \rbrace^* $ to itself. Hence we get one function from word to word per state. Moreover, since these functions have the same domain and codomain, we can compose them as we want. Note that the composition corresponds in the automaton to the plug-in of the output of a run to the input of another. Namely $\rho_{ab} = \rho_b \circ \rho_a$ can be seen as

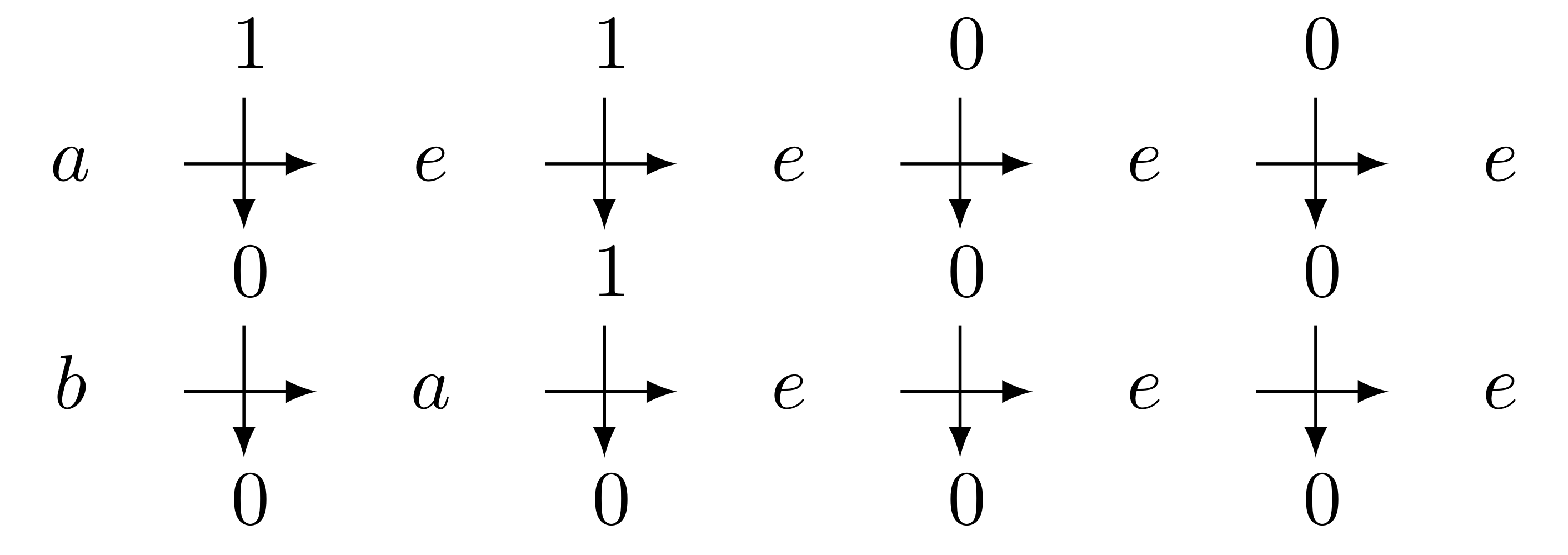
This structure where object can be compose together is called a semigroup. The most well known semigroup is certainly the set of positive integer (because the addition of two such number is always a positive integer), but in computer science we also use quite often the semigroup of words (the concatenation of two words is also a word), and we can think to many other examples. The theory of semigroups is a wide area intertangling math and informatics, but one is generally more familiar with group theory, where the elements can always be inversed.

In our setting, generating a group means that each function has to be bijective, i.e. that every state induces a function that can be inverted.

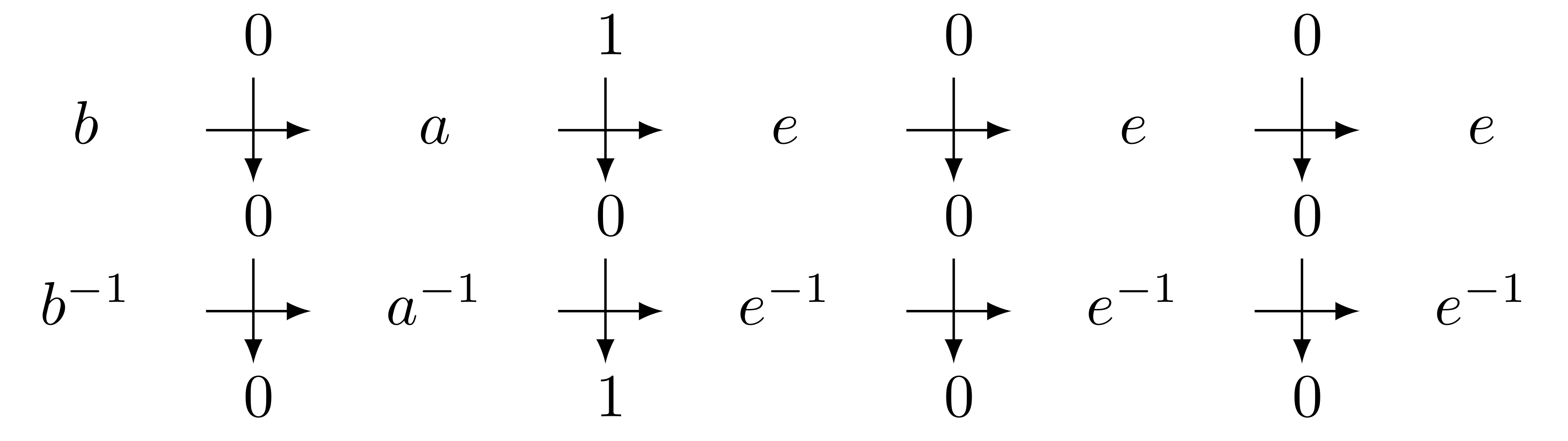
This can be easily verified on the automaton: it is equivalent to require that every state induces a permutation on the alphabet. This is the case for the Grigorchuk automaton (for instance $a$ flips $0$ and $1$), so we can study the group generated by the Grigorchuk automaton, henceforth called the Grigorchuk group.

A Mealy automaton which cannot generate a group. For instance $p$ sends 1 and 2 onto 1, and thus cannot be inverted.

Infiniteness of the Grigorchuk group

For the Grigorchuk group lots of properties are known. For instance we can prove that it infinite :

First, we can see that $e = \mathbb{1}_{\Sigma^*}$ because $e$ is a sink state which copies the input word on the output.

We are going to construct an infinite number of elements via a morphism~$\eta$ defined by:

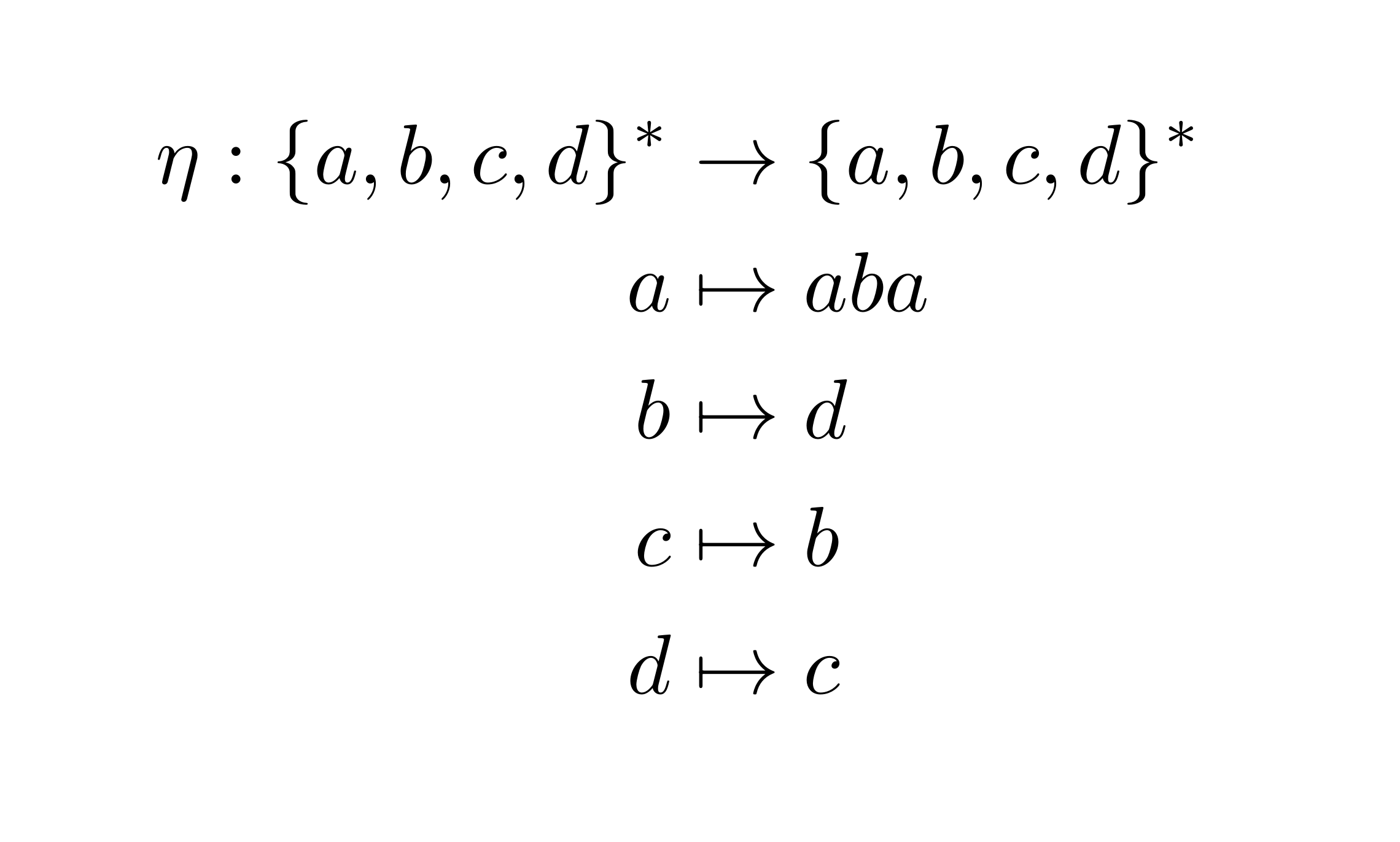
Lemma The elements $\eta^{\ell}(a)$ are pairwise different in the Grigorchuk group.

Proof We show that the $\eta^{\ell}(a)$ act differently on $1^\omega$. We have:

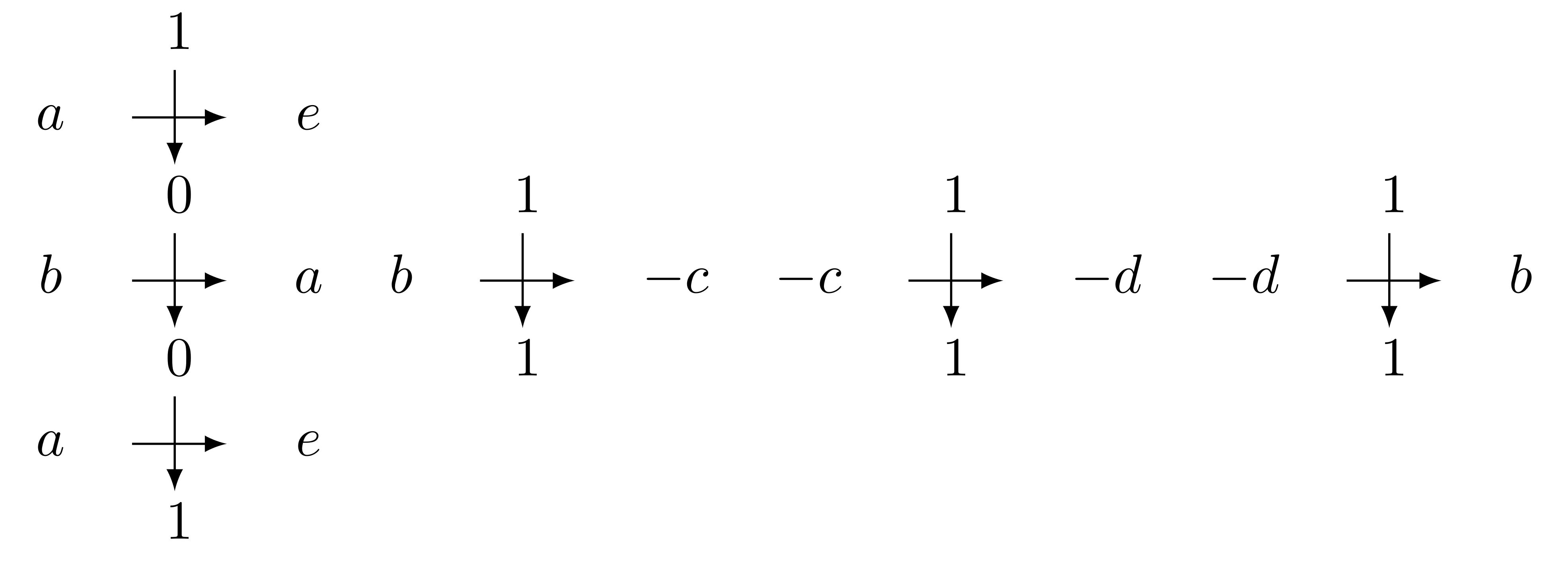
So, as $e$ acts like the identity in the group, it can be ignored when it appears in a word, we have:

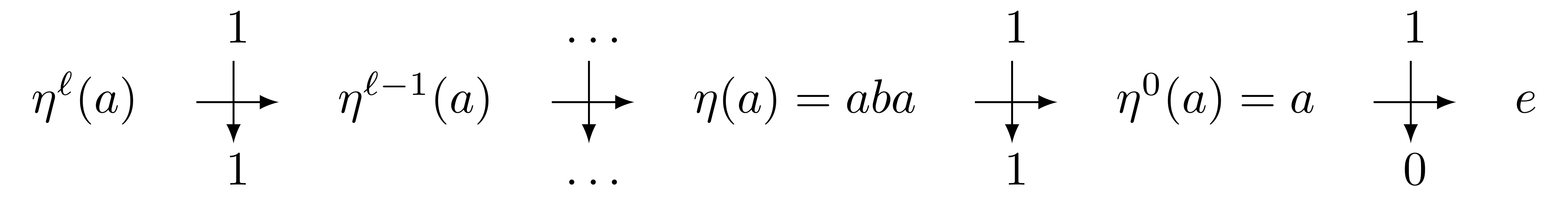
hence every $\eta^\ell(a)$ acts differently on $1^\omega$, so they represent different elements in the group.

We have proved:

Corollary: The Grigorchuk group is infinite.

The Burnside Problem

Now, why would one wants to study such groups? Because it is an infinite Burnside group. Let’s elaborate:

the order of a element $g$ is the smallest positive integer~$n$ such that $g^n$ is the identity in the group. When such an integer exists we say that $g$ has finite order, infinite otherwise.

For instance in $(\mathbb{Z}/12\mathbb{Z},+)$, $5$ has order $12$ because $5+5=10$, $10+5 = 3$, $3+5=8$, $8+5=1$, $1+5=6$, $6+5=11$, $11+5 = 4$, $4+5 = 9$, $9+5=2$, $2+5=7$, $7+5=0=e$. In the same fashion $2$ has order 6 and $8$ has order $3$.

On the other hand, for the group of integers $\mathbb{Z}$, zero is the only element of finite order since the repeated sum of the same integer goes to plus or minus infinity.

It is quite clear that if a group has an element of infinite order (and hence contains a copy of $\mathbb{Z}$ has a subgroup), then it has to be infinite (if $g$ has infinite order, then $\lbrace g^k, k \in \mathbb{Z} \rbrace$ is infinite). The reciprocal gives that a finite group has only elements of finite order.

At the beginning of the XX${}^{th}$ century, people only knew finite groups and infinite groups with elements of infinite order.¹ Hence the question of Burnside:

Question, Burnside (1902): Can a finitely generated group have all elements of finite order and be infinite?

This question became central in group theory and was solved for several classes of groups (for instance it is not hard to see that when the group is commutative the answer is no).

The solution was found in 1964 by Golod and Shafarevich, who gave an explicit example of a finitely generated group with all elements of finite order and infinite (henceforth called infinite Burnside group. However this example is very complicated and requires deep results in field theory, and, as these groups are on the edge between finiteness and infiniteness, people continued to look for examples.

We are now going to prove that the group generated by the Grigorchuk automaton is an infinite Burnside group.

One of the crucial observation for our proof is that the subgroup generated by $b,c,d$ is finite: $\langle b,c,d \rangle = \mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/2\mathbb{Z}$. The relations are:

$bc=cb=d ~;~ bd=db=c ~;~ cd=dc= b.$

The proof is a simple verification and can be done with cross diagrams or via computer assisted computations.

Let us recall that the conjugate of $g$ by $h$ is the group element $h^{-1}gh$. We need the small lemma:

Lemma If $g$ has finite order $n$, then so does each of its conjugates.

Proof: We compute:

$(h^{-1}gh)^n = h^{-1}ghh^{-1}gh … h^{-1}gh = h^{-1}g^nh =h^{-1}e h = e$.

So $h^{-1}gh$ has order less than $n$, we get the other inequality by symmetry: $g$ is conjugate to $h^{-1}gh$ by $h^{-1}$.

We now have all the tools we need to prove

Theorem: The group $\langle\mathcal{G}\rangle$ has every element of finite order.

Proof: Let $g \in \langle\mathcal{G}\rangle$. We are going to do an induction on the length of the shortest representative of $g$ on $Q^*$. Let $\ell$ be this shortest length and $\mathbf{w}$ be a word on $Q$ of length $\ell$ representing $g$ in $\langle\mathcal{G}\rangle$. As the product of two element of $S := Q \setminus \lbrace a \rbrace$ is an element of $S$, we can assume that $\mathbf{w}$ is written as an alternation of an $a$ and a letter of $S$. One can show² for initialisation, that if $\ell < 3$, then $g$ has finite order.

Assume $\ell$ is odd. If $\mathbf{w}$ starts with an $a$, then $\mathbf{w}= a\mathbf{u}a = {\mathbf{u}}^{a}$ (since $a^{-1}=a$), with $\mathbf{u}$ a word on $Q$ of length $\ell - 2$. Hence we can use the induction of $u$, and since conjugation does not change the order (Lemma above), $g$ has finite order. If $\mathbf{w}$ starts with $p \in S$, then $\mathbf{w} = p\mathbf{u}q$, $q\in S$. We can conjugate by $p^{-1}$ : ${g}^{p^{-1}} = p^{-1}p \mathbf{u} q p$. The word $\mathbf{u}r$ has length at most $\ell -1$ (since $q.p = r \in S$), whence the order of $g$ (which is equal to the order of $\mathbf{u}r$) is finite order using the induction hypothesis.

Now is $\ell$ is even. By conjugation we can assume that $\mathbf{w}$ starts with an $a$. We are going to split the analysis into sub-cases depending on the length of $\mathbf{w}$. If $4$ divides $\ell$, then $\mathbf{w} = a w_1 a u_1 a w_2 a … a w_{\ell/4} a u_{\ell /4} $ and we can group the letters of $w$ into blocks $a w_i a$ and $w_j$. As $\mathbf{w}$ has an even number of $a$, $\mathbf{w}$, can be decomposed as $ (\mathbf{w_{ 0}},\mathbf{w_{ 1}})()$³ where $\mathbf{w_\epsilon}$ ($\epsilon \in \lbrace 0, 1 \rbrace$) have length at most $\ell/2$, since blocks $aw_ia$ can be decomposed as $aw_ia = (s,t)$ with $s,t \in Q$. So, the order of $g$ is the lowest common multiple of the orders of $\mathbf{w_\epsilon}$, finite by the induction. Finally, if $\ell= 4j-2$, we consider $g^2$, represented by $\mathbf{ww}$.

• if $\mathbf{w}$ contains a letter $d$, then the length of $(w_{\epsilon})$ is lesser or equal to $ 4j-3$ and we can conclude.
• if $\mathbf{w}$contains a letter $ c$ then the words $\mathbf{w_{\epsilon}}$ are either of size lesser or equal to $4j-3$, or contain a $d$, and we conclude using the previous case on $\mathbf{w_\epsilon}$.
• otherwise, the word $\mathbf{w}$ is a power $ab$, hence of finite order.

Using the corollary above, we get:

Theorem: The group $\langle\mathcal{G}\rangle$ generated by the Grigorchuk automaton $\mathcal{G}$ is an infinite Burnside group.

Conclusion

Among the interests of this proof are its shortness and elementariness: we have not used any theorem that goes further a first lecture in group theory.

Moreover, these groups generated by Mealy automata have given several other interesting examples, among which are the first groups with intermediate growth (solving Milnor Problem), non uniform exponential growth (solving Gromov Problem), or Amenability but not exponentially amenability (solving Day Problem).

On the computer science side, some graphs associated with Mealy automata are conjectured to by families of expander graphs.

My research involves linking the structure of the automaton and the properties of the group it generates. With co-authors we proved that some shapes in the Mealy automaton forbids the group it generates to be infinite~Burnside.

Footnotes