Introduction ludique à la sémantique des jeux
22 Sep 2017Hi! This post by Clément Jacq is about game semantics. It is in French but you can check out the slides in English here, and a more in-depth survey here.
Bonjour à tous pour ce premier vrai post en français sur semidoc. Et c’est Clément Jacq (ancien responsable du séminaire) qui nous parle de sémantique des jeux, inspiré de son exposé du printemps. Vous pouvez retrouver le support de l’exposé ici et un texte plus approfondi là.
Sémantique des jeux antique
La sémantique des jeux a d’abord été introduite dans les années 50 par Lorenzen and Lorenz. L’objectif était de lier les notions de vérité et de validité de la logique classique à des concepts de théorie des jeux telles que l’existence de stratégie. L’intuition est la suivante . Pour chaque formule, on construit un jeu d’arêne à deux joueurs :
- Les deux joueurs sont le Vérificateur et le Falsificateur.
- chaque connecteur et chaque constante de la formule sont des positions du jeu “contrôlées” par l’un des deux joueurs.
- Lorsque le jeu est dans une position qu’un joueur contrôle, celui-ci peut choisir la position suivante parmi les positions disponibles.
- La partie se termine quand il n’y a pas de choix pour le joueur en cours, celui-ci est alors désigné vainqueur.
- La formule est vraie si et seulement si il existe une stratégie gagnante pour le Vérificateur. C’est à dire que quelque soient les choix du Falsificateur, le Vérificateur peut toujours orienter la partie vers une position finale sous son contrôle.
Voici un exemple du jeu associé à la formule de logique propositionnelle $(V \cup F) \wedge \neg (F \cup V)$
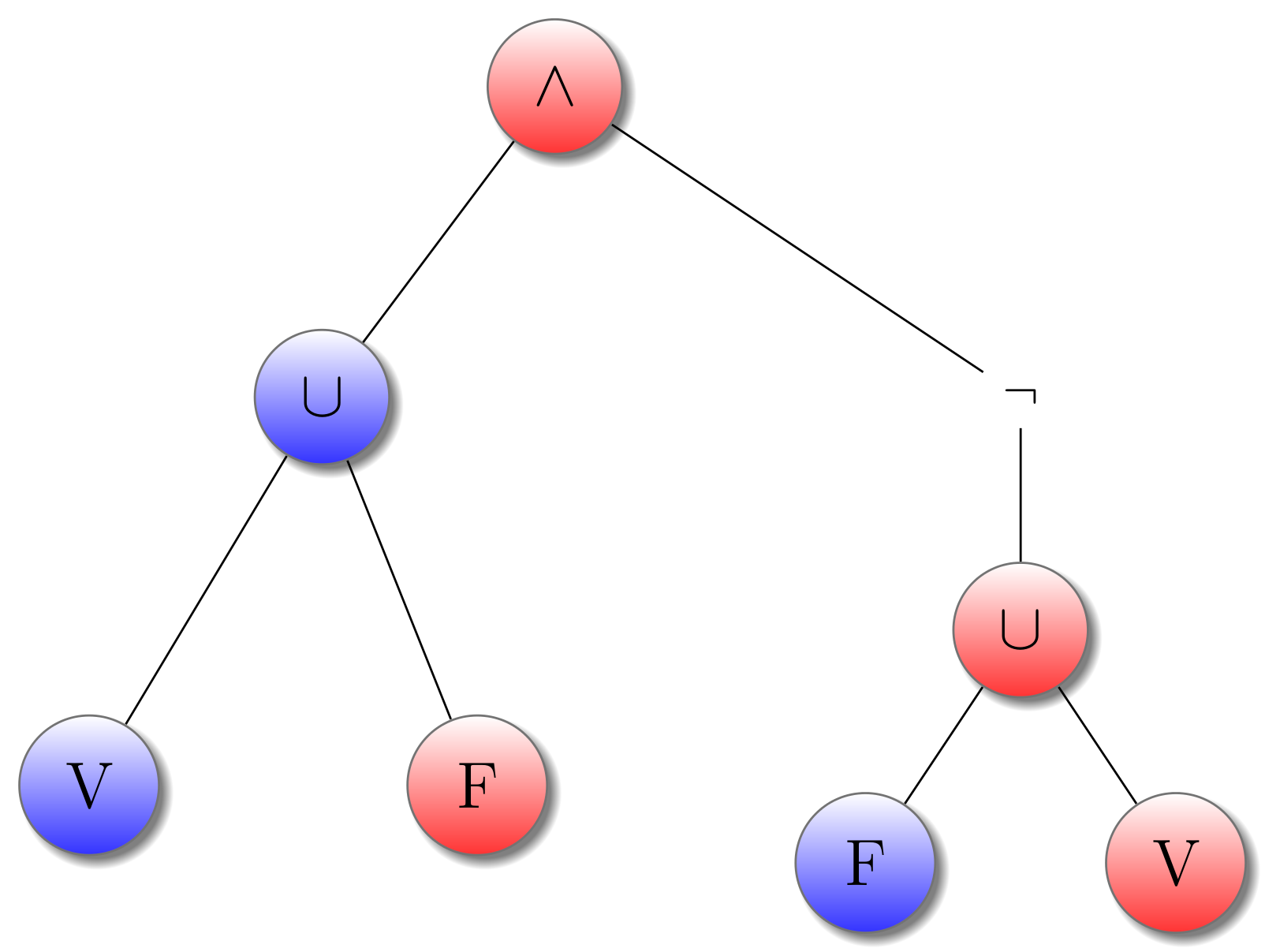
Les atomes Vrai et $\cup$ sont associés au Vérificateur (en bleu) et les atomes Faux et $\wedge$ au Falsificateur (en rouge). A noter le role particulier de la négation qui inverse les possesseurs des positions de son sous-arbre. La formule est ici fausse car le falsificateur peut jouer dans la branche de droite sans laisser au Vérificateur une possibilité d’influer sur les positions.
Des stratégies et des jeux
On va s’intêressé ici à une sémantique des jeux plus moderne créée à la suite des travaux de Girard sur la logique linéaire en 1987. De nombreux travaux dans ce domaine sont apparus dans manière simultanée dans les années 90. Citons notamment ceux d’Abramsky, de Blass, de Hyland ou de Ong. Une des particularités de la logique linéaire est qu’elle permet de bien retranscrire le fonctionnement d’un programme. Pour simplifier cette présentation, nous modéliserons directement par nos jeux un langage de programmation simple.
Définition Un jeu simple est un jeu d’arbre enraciné à deux joueurs, que l’on appelera Opposant et Joueur, qui joue chacun leur tour et dont les parties sont de taille finie. De plus nous ajoutons la règle que l’Opposant est toujours le premier à jouer.
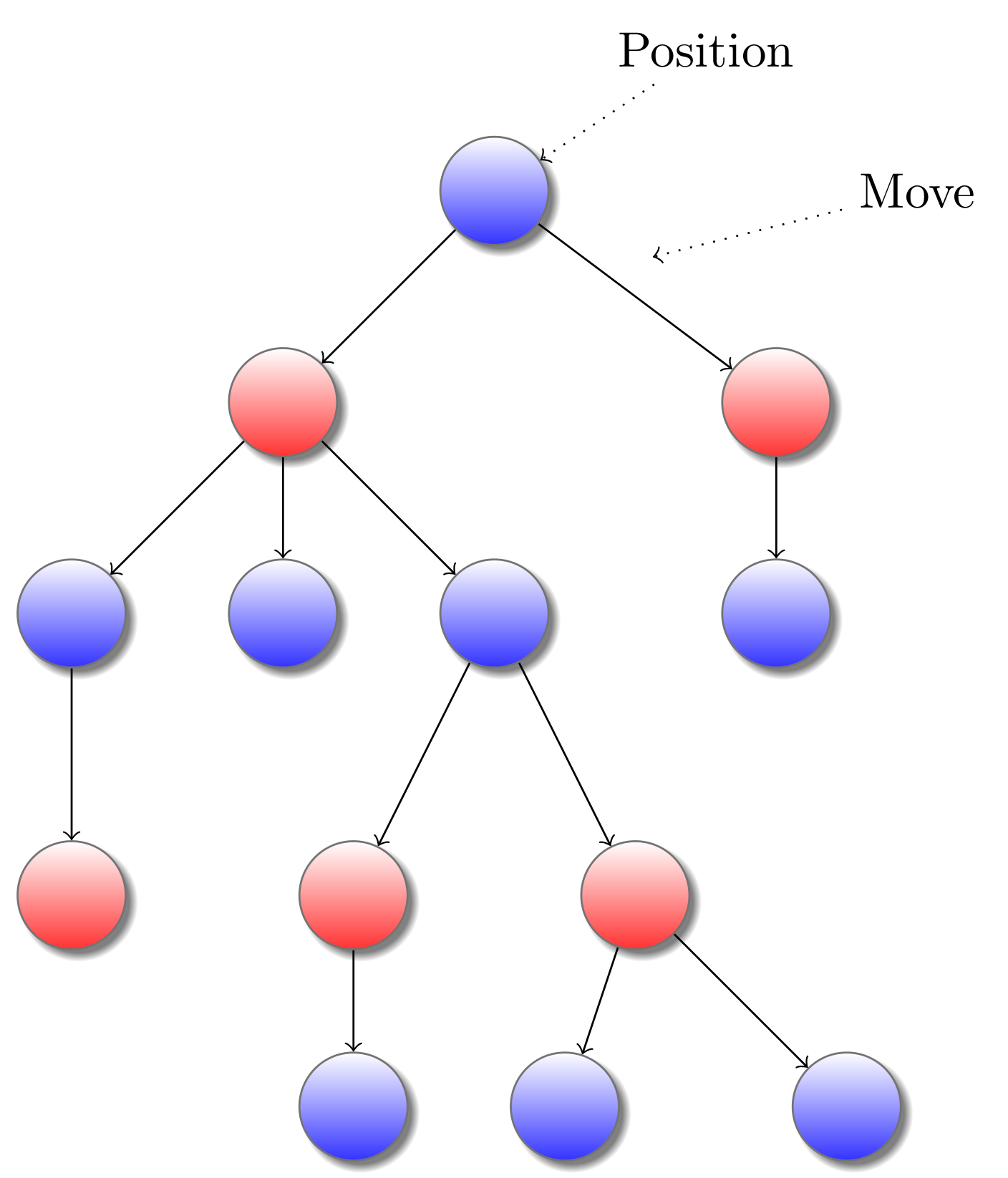
Voici un exemple de jeu simple, les noeuds sont appelés des positions et les arêtes des coups. Les positions bleues sont celles où l’Opposant s’apprête à choisir un coup.
Avec cette notion de jeu, nous avons besoin d’une notion de stratégie. Par usage, on se place du point de vue de Joueur, c’est à dire qu’une stratégie est un ensemble indiquant à Joueur comment jouer. Plus formellement:
Définition Une stratégie pour Joueur d’un jeu G est un ensemble de parties de $G$ clos par préfixe ( c’est à dire que la stratégie ne contient des informations que sur les parties qu’on peut atteindre par celle-ci), et déterministe ( à chaque position, Joueur n’a au plus qu’un seul choix qui est dans la stratégie)
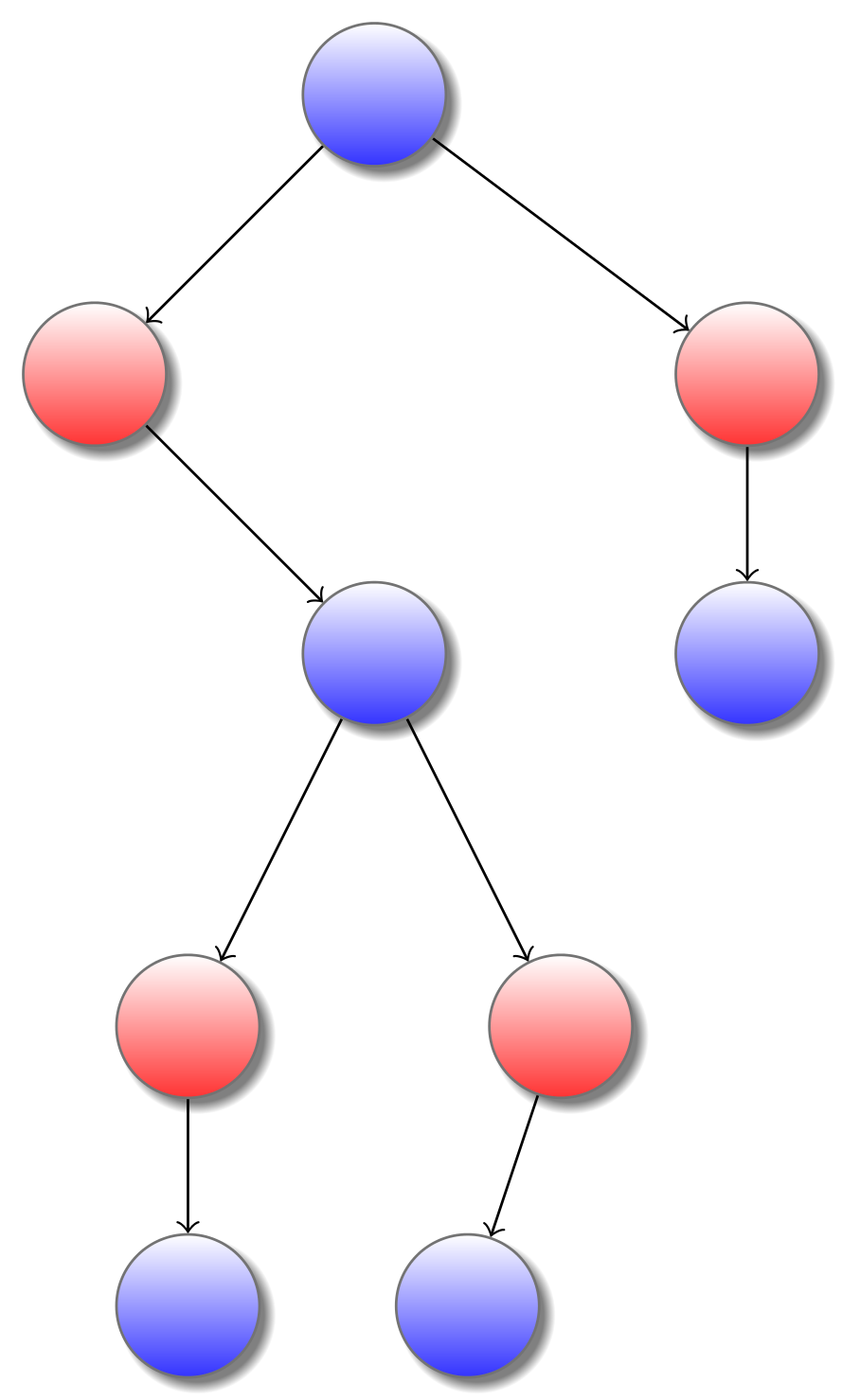
Voici un exemple de stratégie pour le jeu montré précédemment. On peut noter qu’il s’agit d’un sous-arbre du jeu en question.
Ceci nous donne les bases pour construire nos premiers programmes .
Modéliser de simples programmes
Le langage de programmation que nous allons modéliser par nos jeux est un language fonctionnel typé (par exemple Caml). L’idée générale est la suivante :
- Chaque type du langage correspond à un jeu. (On peut donc imaginer un jeu Bool, un jeu Int,…)
- Chaque programme valide de type A correspond à une stratégie du jeu $A$.
Une bonne intuition à noter pour la suite est que les rôles des deux joueurs du jeu peuvent représenter l’Environnement et le Programme dans l’interaction. C’est pour cela qu’on peut voir un programme valide comme une stratégie pour Joueur, car une stratégie indique alors les comportements raisonnables du Programme face à l’Environnement.
 |
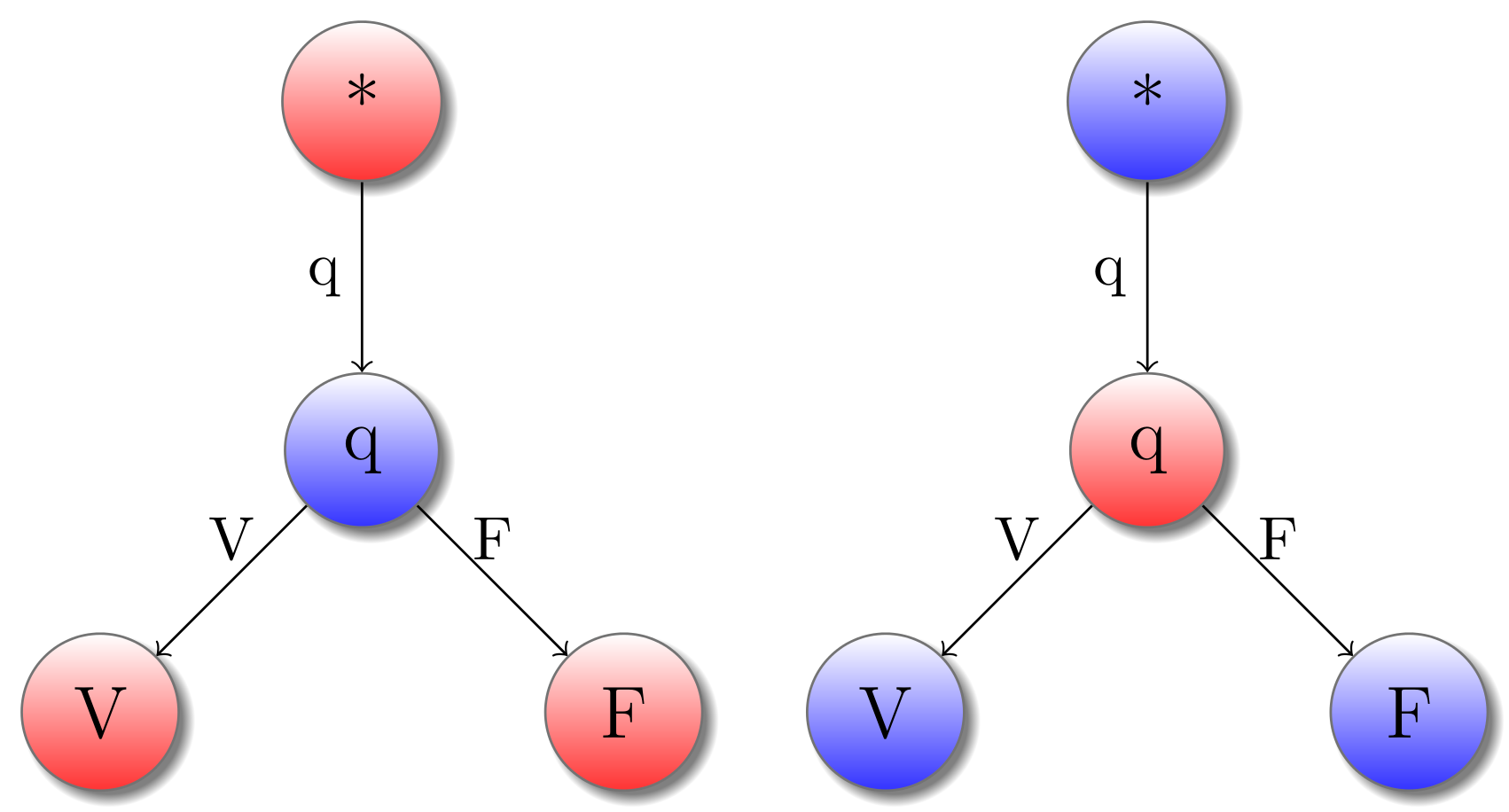
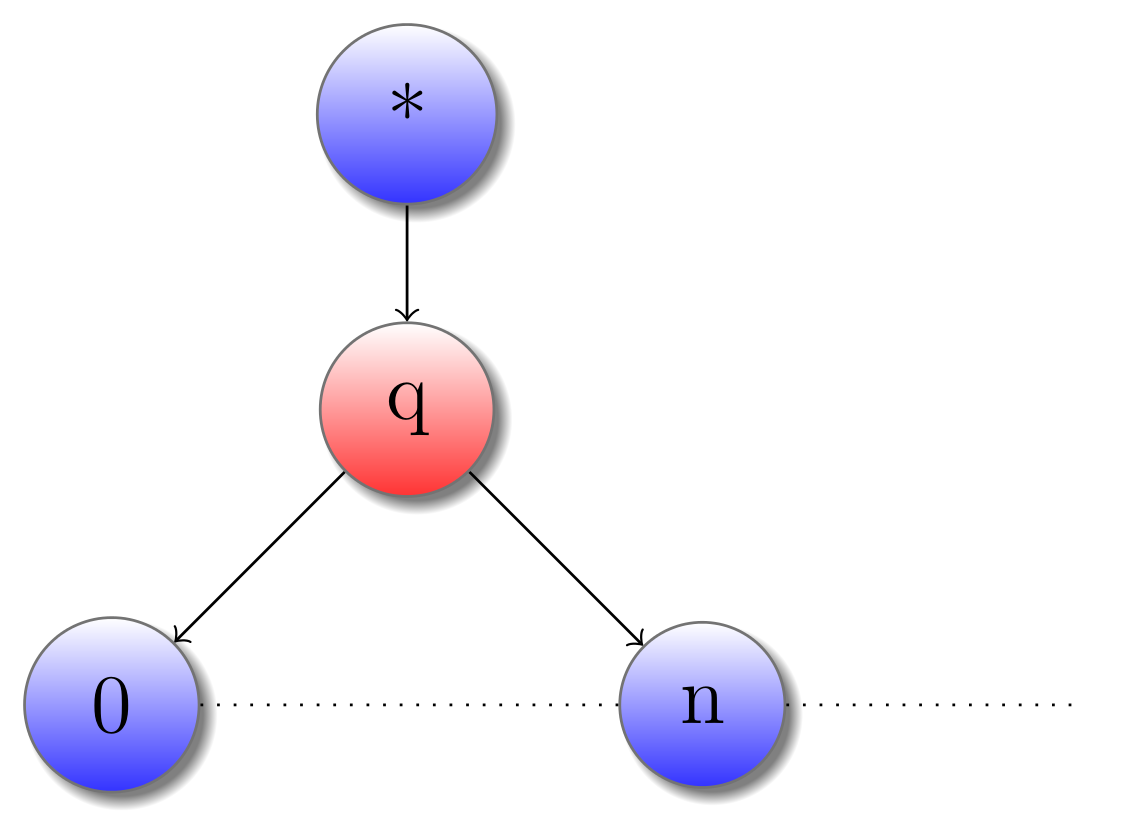 |
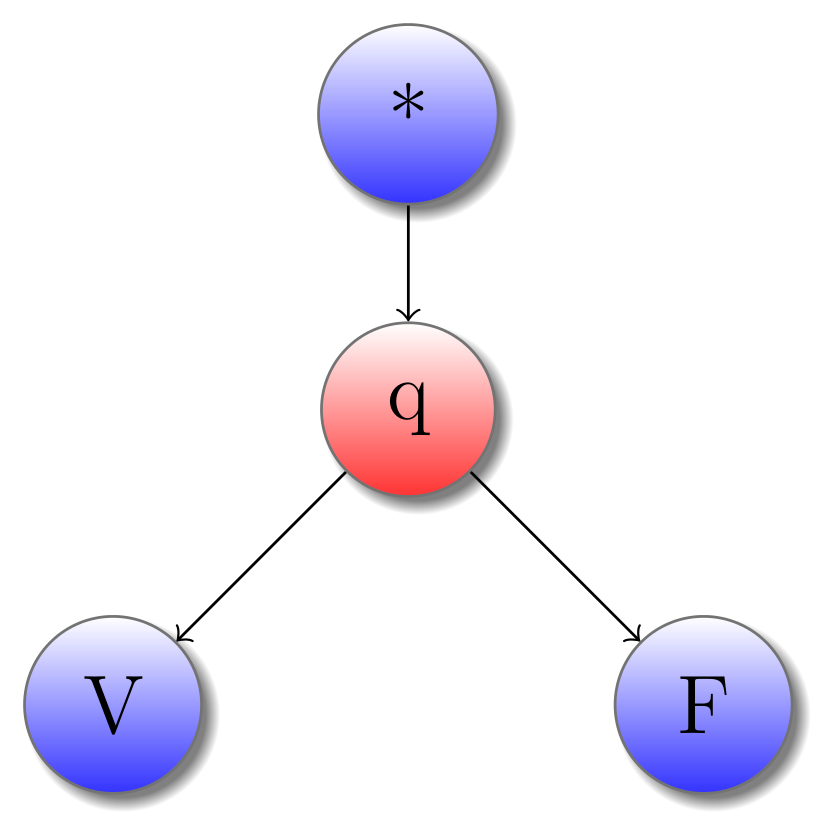
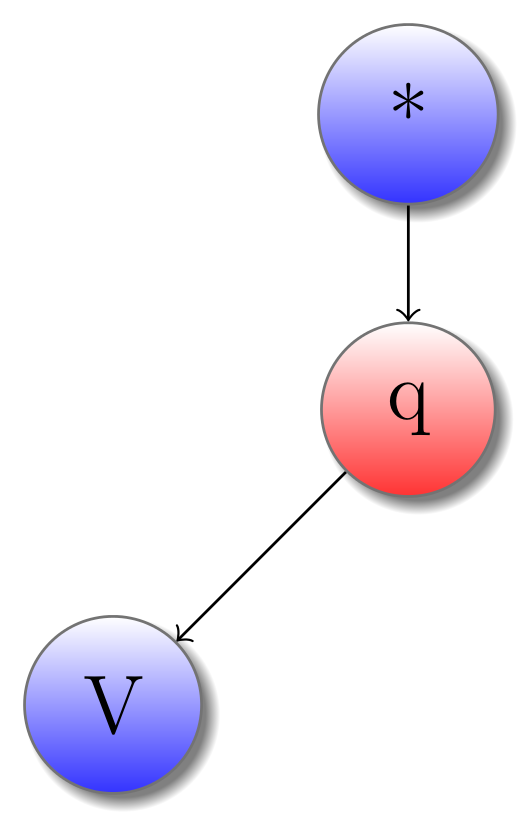
Voici deux exemples deux jeux, réprésentant les types simples que sont les booléens et les entiers. Une stratégie dans un de ces types représente tout simplement une constante, l’unique moment ou Joueur doit faire un choix étant le choix de la valeur. Par exemple, voici la stratégie associée à la constante Vrai :
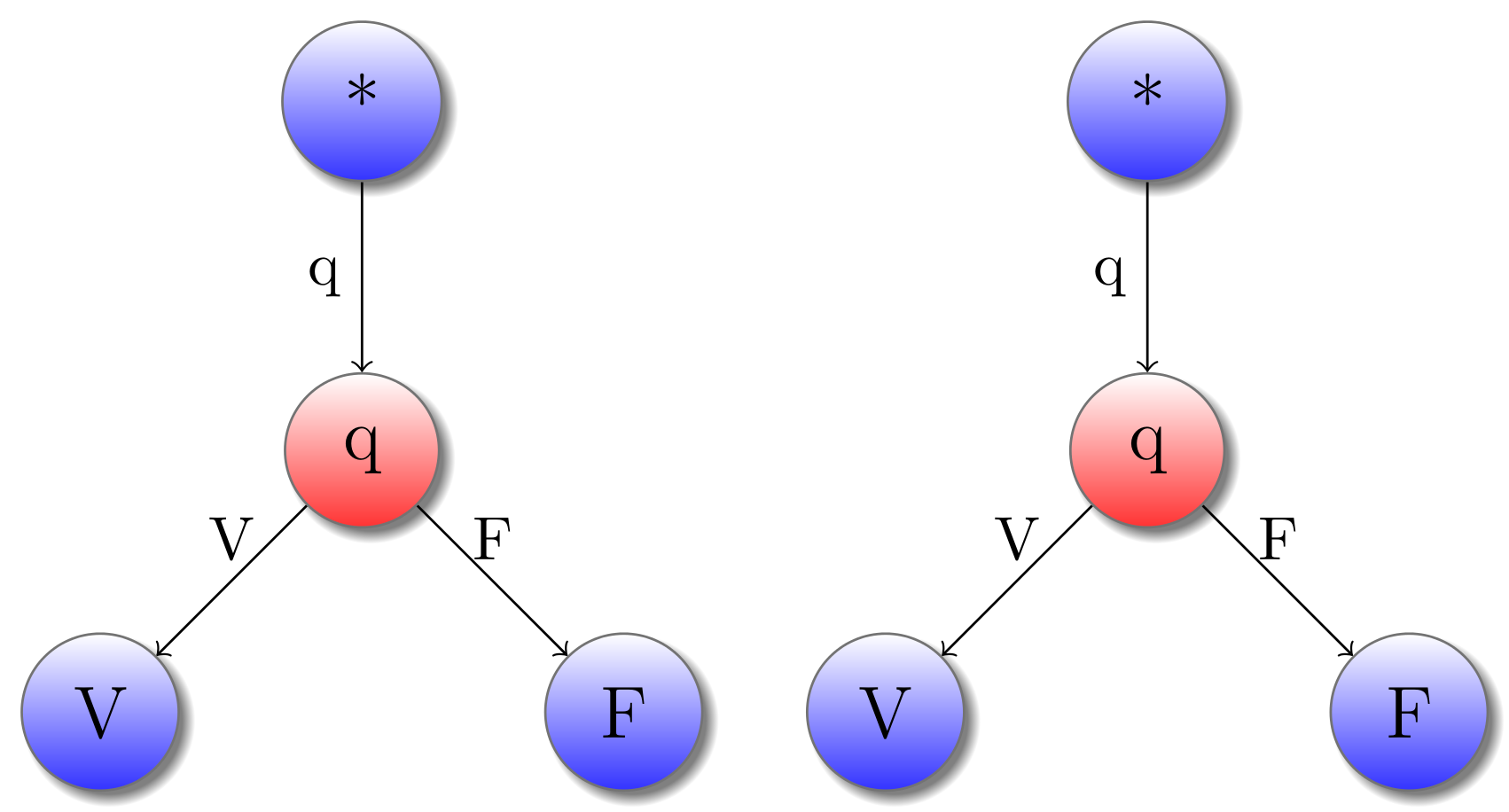
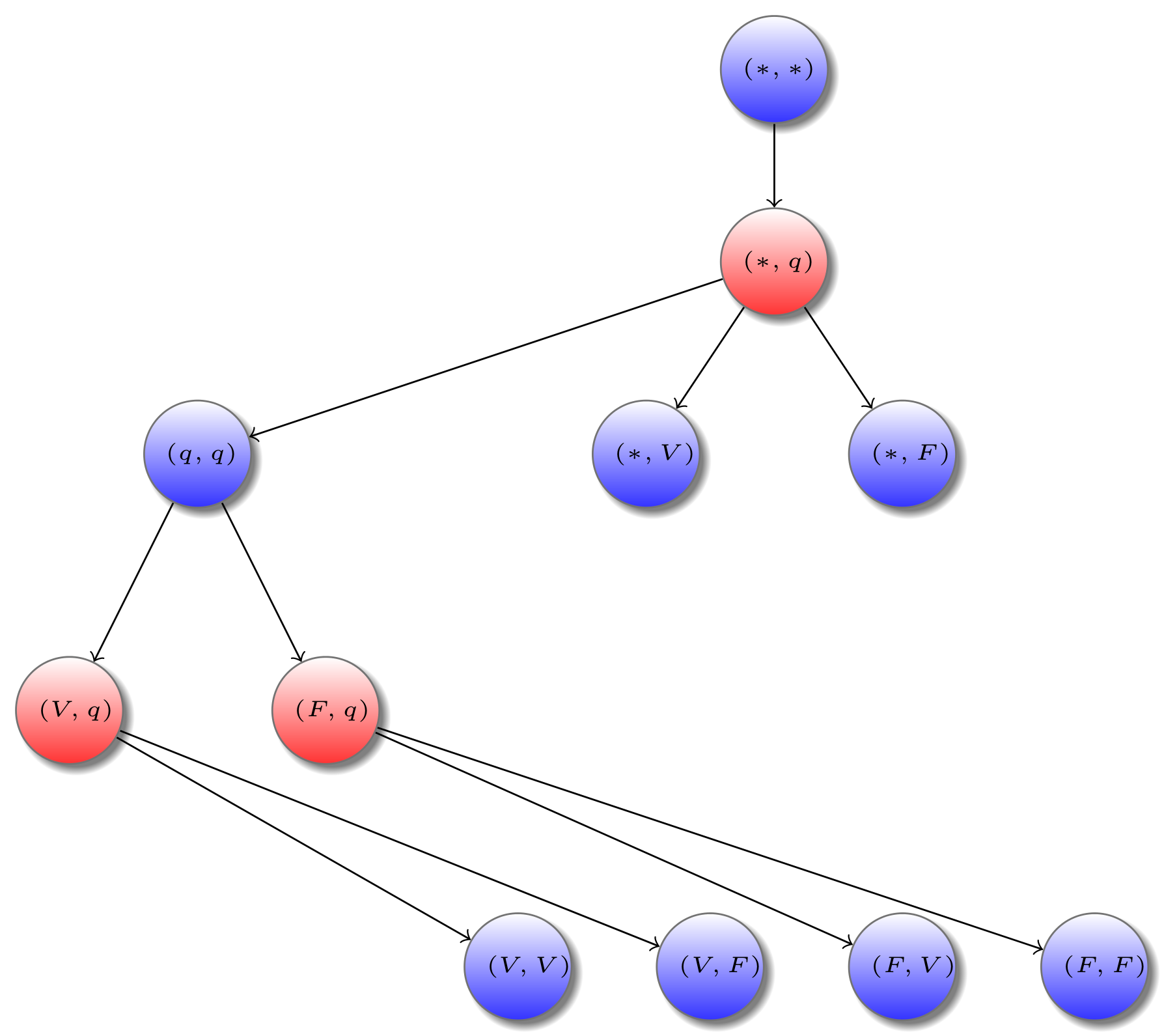
Maintenant que nous avons mis en place les types simples de constante, mettons en place des types un peu plus complexe. Commençons par les paires (et plus généralement les n-uplets). L’intuition est extrèmement simple. Pour construire le type des paires de deux booléens, on prend le jeu Bool en double et on peut jouer dans les deux instances au choix, obtenant au final une paire de booléens.
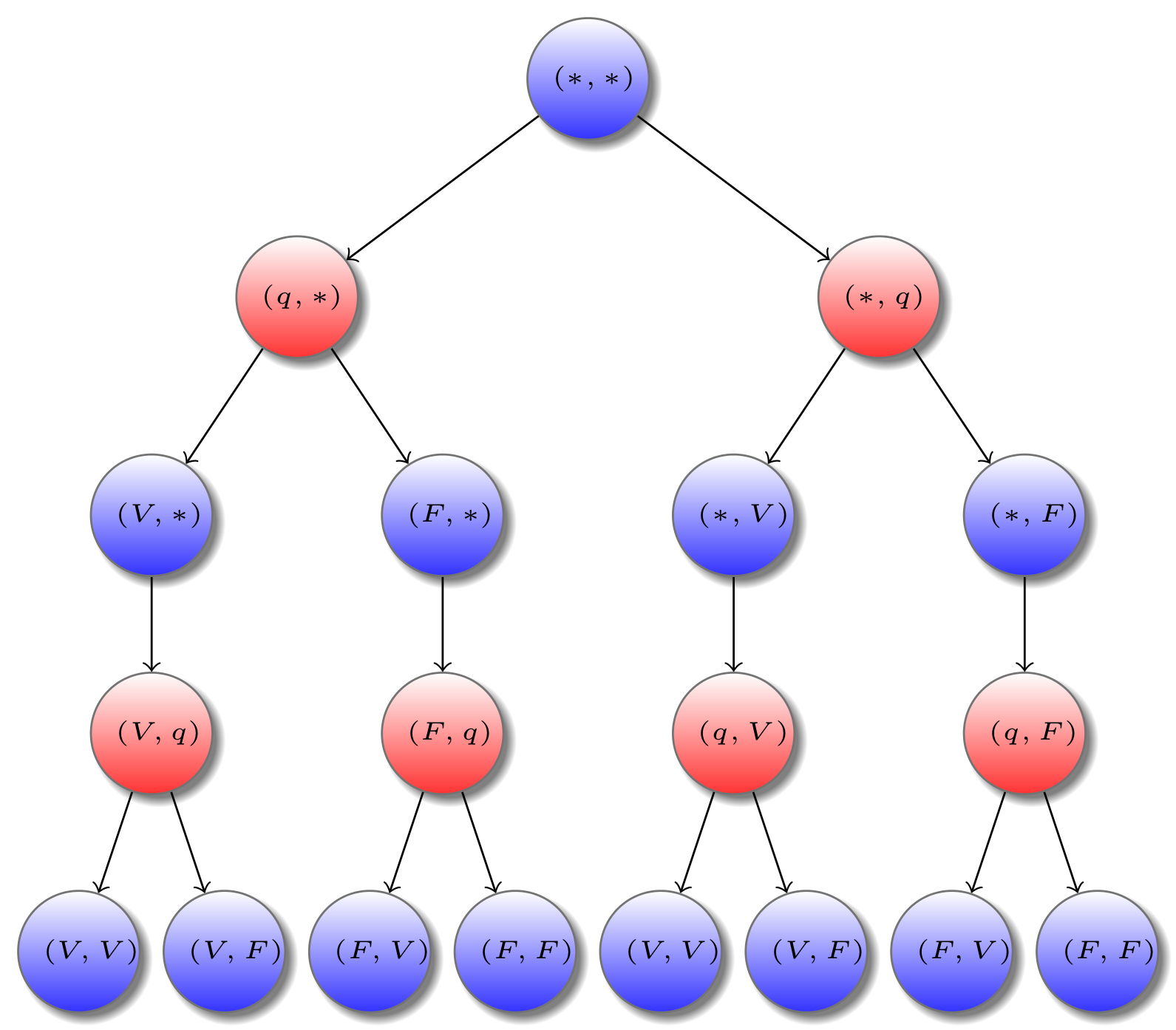
Il est bon de noter que cela ne forme pas un jeu au sens où nous l’avons défini. En effet, il n’y a pas une unique racine et l’ordre des coups entre les deux jeux n’est pas clair. La définition formelle du jeu$Bool \otimes Bool$ est un peu plus complexe :
Introduction des fonctions
Jusqu’à présent, tous les programmes que nous avons décrits sont quasiment triviaux. il ne s’agissait que de constantes. En terme d’interaction, ces programmes se comportent de la manière suivante : Opposant/l’Environnement demande des valeurs spécifiques et Joueur/le Programme les lui fournit.\
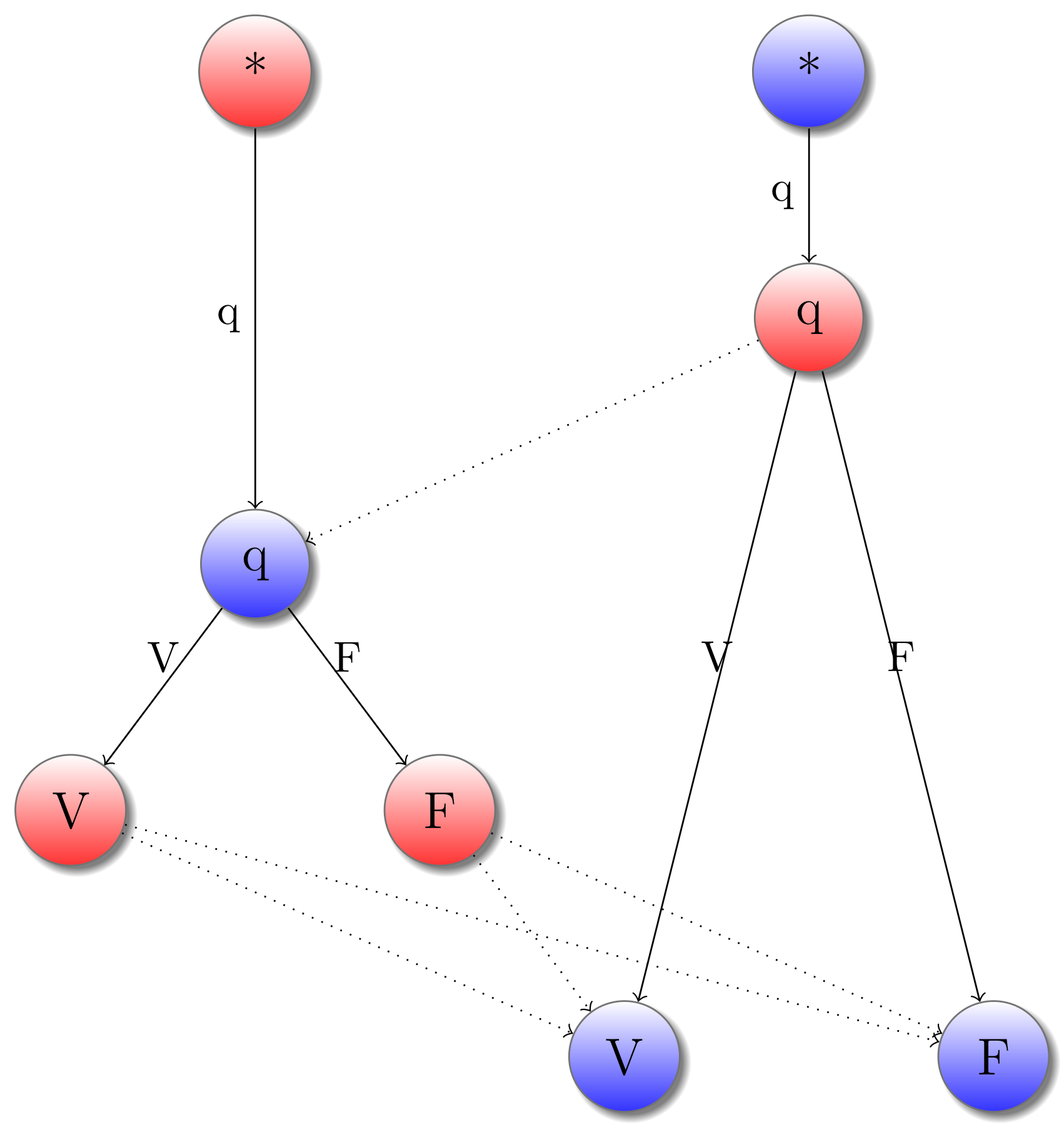
Pour les fonctions, l’interaction inverse va aussi avoir lieur. Le Programme va demander des arguments qui vont être fournis par l’Environnement. Intuitivement, en se souvenant du rôle de la négation en sémantique des jeux historique, le jeu de type $A\rightarrow B$ peut etre vu comme $(\neg A) \otimes B$. Prenons l’exemple du jeu $Bool \rightarrow Bool$ :
Comme indiqué par l’intuition, la partie gauche du jeu, qui correspond à l’argument est inversée. Pour clarifier un peu le dessin, ajoutons en pointillé les endroits ou l’on peut passer d’un jeu à l’autre tout en respectant les règles d’alternance des jeux simples :
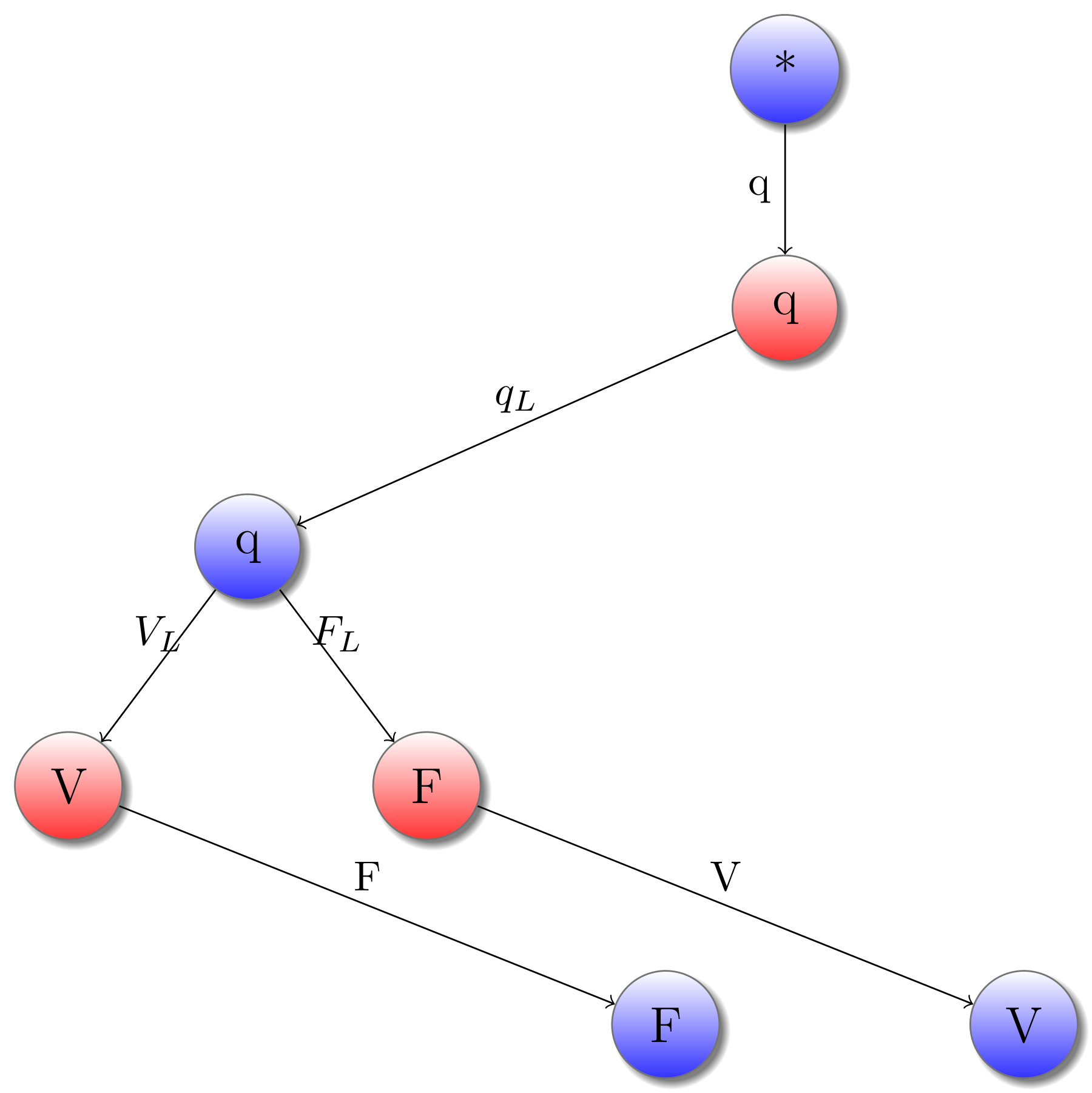
Ce jeu donne bien l’intuition des fonctions booléennes possibles. Une fois que l’environnement a demandé le résultat, le joueur peut soit répondre immédiatement ( fonction constante), soit demander un argument avant de répondre. Voici par exemple la stratégie correspondant à la Negation booléenne :
Comme dans le cas des paires, le véritable jeu est une construction plus complexe
En conclusion de cette partie, voici une partie de la stratégie associée au OR booleen dans une représentation plus légère indiquant les coups joués dans l’ordre et dans le sous-jeu dans lequel ils sont joués :
Il est important de noter que cette partie ne correspond qu’a une version possible du programme OR. En effet, un choix a lieu lors de l’implémentation d’un OR; le choix du premier argument à étudier. Il y a donc plusieurs programmes pour le OR et donc plusieurs stratégies.
Stratégie de composition pour la composition de stratégies
Puisqu’il est possible et même fort utile de composer des fonctions, notre modèle doit pouvoir composer les stratégies de manière facile. Cette composition se construit en parcourant toutes les paires de parties des deux stratégies, (c’est à dire tous les cas possibles des deux fonctions).
Prenons une partie d’une stratégie $\sigma :A \rightarrow B$ et une partie d’une stratégie $\tau : B \rightarrow C$ telles que leurs composantes en $B$ sont égales. Intuivement, cela revient à s’intéresser au cas où l’argument de $\tau $ correspond au resultat de $\sigma$. L’idée est alors de réorganiser les deux parties en fonction de leur composante commune, avant d’effacer celle-ci. La représentation graphique montre ce processus.
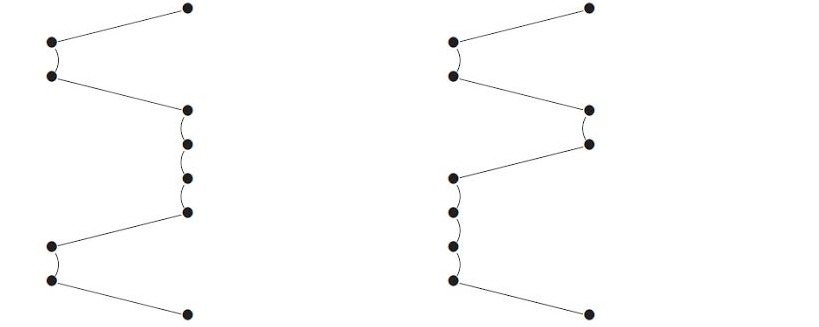
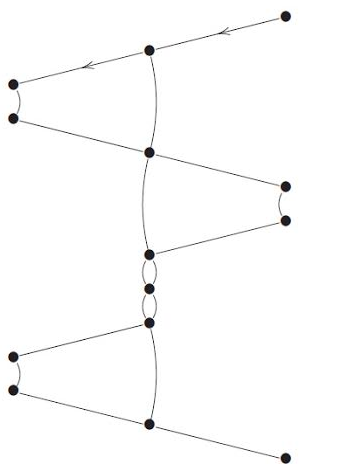
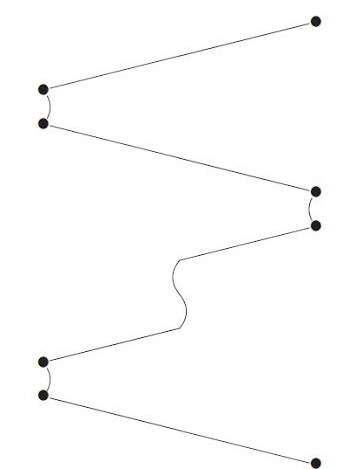
Cette méthode de composition est aussi la manière dont est représentée l’application d’une fonction à un argument, l’argument étant vu comme une stratégie constante de son type.
Pour quelques blocs de plus
Test
Maintenant que nous avons les bases d’un bon langage fonctionnel, ajoutons quelques structures de controle. Commençons par la plus simple, le test. L’intuition pour cette fonction est très simple. Elle nécessite trois arguments, dont un booleen qui représentera le test proprement dit. La fonction commence par demander la valeur de ce booleen. S’il est Vrai, alors elle demande puis renvoie la valeur du premier argument restant. Sinon, elle demande puis renvoie le second. Voici les représentations de deux parties de cette stratégie, dans le cas d’arguments entiers :
A noter que puisque notre langage est typé, c’est aussi le cas du test.
Il existe donc toute une gamme de fonctions de test, une par type.
Boucle
Pour terminer, nous nous interesserons à la modélisation des boucles. Pour ce faire, nous devons introduire deux nouvelles structures, le $!$ et le $?$. Pour un jeu $A$, $!A$ est le jeu basé sur $A$ dans lequel l’Opposant est autorisé à revenir en arrière et à rejouer des coups ( forçant Joueur à y répondre). $?A$ fonctionne de la même manière, mais pour Joueur.
Dans une stratégie quelconque d’un tel jeu, Joueur, si il se retrouve plusieurs fois devant le même choix (par répétition de mouvements d’Opposant), peut répondre de manière différente à chaque fois. Cela ne contredit pas le déterminisme, car on s’intéresse ici au déterminisme dans l’arbre correspondant à $!A$ qui est beaucoup plus complexe que celui de $A$. Si la $même$ position est jouée deux fois par Opposant, il y aura deux noeuds distincts dans l’arbre de $!A$.
Pour se rendre compte de ce qu’il est effectivement possible de faire, voici un exemple de partie de $!(Bool \rightarrow Bool)$.
Dans le cas de la boucle whle, le jeu associé va utiliser à la fois $!$ sur la partie gauche de la fonction et $?$ sur la partie droite. C’est donc joueur qui sera au contrôle des retours en arrière.
La fonction sera de type et fonctionne de la manière suivante. Joueur commence par demander la valeur du test booleen, s’il est vrai, les calculs reprennent dans $A$ jusqu’à ce que joueur considère qu’il doit demander de nouveau un test, ce qui le fera recommencer les calculs si ce nouveau test est vrai. Et ainsi de suite jusqu’à ce qu’un test retourne faux. En ce cas, Joueur conclue la partie en renvoyant le résultat.
Conclusion
Cette présentation n’a abordé que quelques aspects de base de la modélisation des langages de programmation en sémantique des jeux et ne s’est appuyé que sur un modèle particulier. Bien d’autres modèles de jeux existent pouvant modéliser bien d’autres comportements, tels que le non-déterminisme, la concurrence, les Effets, les Références ou les Langages Objets. Pour ce dernier exemple, un langage de programmation orienté Objet, Eriskay a été developpé par Jon Longley en se basant sur les concepts de la sémantique des jeux.