Sturmian words

07 Sep 2017

Hi, this is the second post by Pablo Rotondo. This one is about sturmian words, and sometimes refers to the first post about continued fractions, that you can found here.

---

Sturmian words are infinite words ${\bf{u}}=u_0u_1\ldots\in \mathcal{A}^\infty$ (sequences of symbols $u_i$ from an alphabet $\mathcal{A}$) that have numerous characterizations, as the coding of digital lines, as rotation sequences, minimal complexity sequences…

A first definition

Definition [Sturmian word] Consider $\alpha,\beta \in [0,1)$ with $\alpha$ irrational. We define infinite words $\left(\underline{s}_{\alpha,\beta}(n)\right)_{n\in\mathbb{N}}$ and $\left(\bar{s}_{\alpha,\beta}(n)\right)_{n\in\mathbb{N}}$ by

$$\underline{s}_{\alpha,\beta}(n)= \left\lfloor (n+1)\,\alpha +\beta \right\rfloor - \left\lfloor n\,\alpha +\beta \right\rfloor\, ,$$

and

$$\bar{s}_{\alpha,\beta}(n)= \left\lceil (n+1)\,\alpha +\beta \right\rceil - \left\lceil n\,\alpha +\beta \right\rceil\,,$$

for each $n\in \mathbb{N}$. A binary word ${\bf{u}} \in {0,1}^\infty$ is Sturmian if and only if it is of the form $u_n = \underline{s}_{\alpha,\beta}(n),\,\forall n$, or $u_n = \bar{s}_{\alpha,\beta}(n),\,\forall n$ for some $\alpha,\beta$ as above. The irrational number $\alpha$ is called the slope of the word $\bf{u}$.

Remark Observe that if ${\bf{u}}=\underline{s}_{\alpha,\beta}$

$$\lim_{n\to\infty} \frac{|u_0\ldots u_{n-1}|_1}{n} = \lim_{n\to\infty} \frac{1}{n}\,\sum_{i=0}^{n-1}u_i = \lim_{n\to\infty} \frac{\left\lfloor n\,\alpha +\beta \right\rfloor-\left\lfloor \beta \right\rfloor}{n} = \alpha\,,$$

where $|\cdot|_1$ denotes the number of ones in the word. Thus $\alpha$ represents the frequency of ones. Clearly the same result is true when ${\bf{u}}=\bar{s}_{\alpha,\beta}$ by the same argument.

Sturmian words as circle rotations

The above definition can be seen more intuitively as the binary coding of the trajectory of a point on a circle of circumference $1$. This circle is realized as the interval $[0,1]$ identifying $0$ and $1$, that is, taking fractional parts $x\mapsto {x}$ or, equivalently, modulo one $x\mapsto x \bmod 1$.

Indeed, observe that

$$\bar{s}_{\alpha,\beta}(n)= 1 \Longleftrightarrow n\alpha + \beta \leq m < (n+1)\alpha + \beta$$

for some integer $m$. By taking $\bmod 1$ it is immediately seen that this means that

$$\bar{s}_{\alpha,\beta}(n) = 1 \Longleftrightarrow \{n\alpha + \beta\} \in I_1 := [1-\alpha,1)\,,$$ $$\bar{s}_{\alpha,\beta}(n) = 0 \Longleftrightarrow \{n\alpha + \beta\} \in I_0 := [0,1-\alpha)\,.$$

A similar definition can be done for $\underline{s}_{\alpha,\beta}(n)$ by reversing the close-open in the border of the intervals. In terms of the circle, this reads: start from a point $y_0=\beta$ on the circle and rotate an arc-length of $\alpha$ on each discrete time $y_{k+1} = (\alpha + y_k)\bmod 1$, then code the resulting points by $1$ when they belong to $I_1$ and $0$ when they belong to $I_0$.

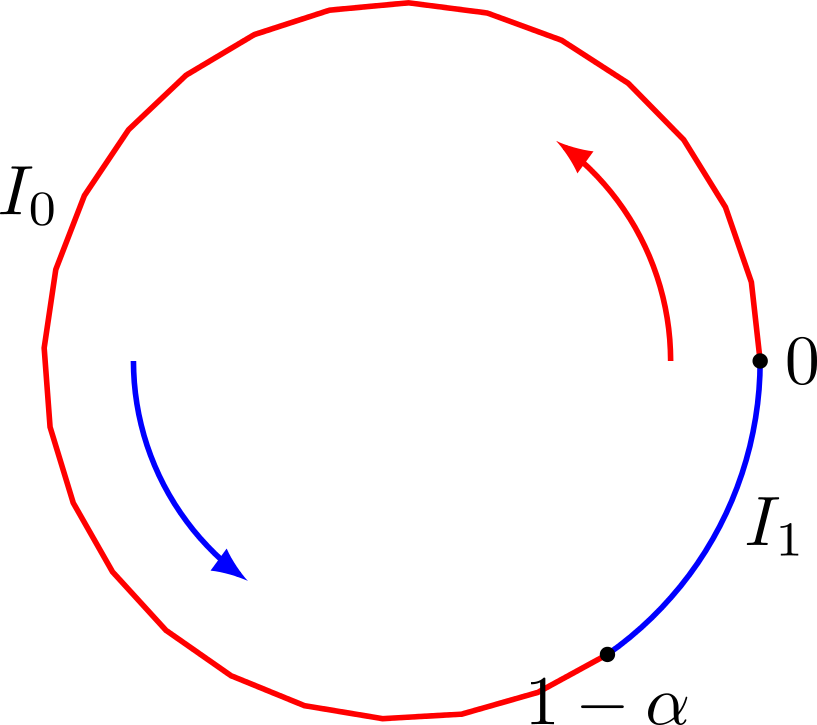
Factors of Sturmian words.

The finite patterns appearing within our infinite words ${\bf{u}}$ are a fundamental object of study in the field of Combinatorics of Words. We say that $w\in {0,1}^m$ is a factor of ${\bf{u}}$ if, for some index $i\geq 0$, we have

$$w_1\ldots w_m = u_i \ldots u_{i+m-1}\,,$$

and say that $m$ is its length.

We have seen that digits in a Sturmian word ${\bf{u}}$ correspond to intervals $I_0$ and $I_1$, this process can be iterated to explain what happens with larger factors $w\in {0,1}^m$. The result being that factors are in correspondance with the circle intervals delimited by

$$0,-\alpha,-2\alpha,\ldots,-m\alpha\,,$$

modulo $1$.

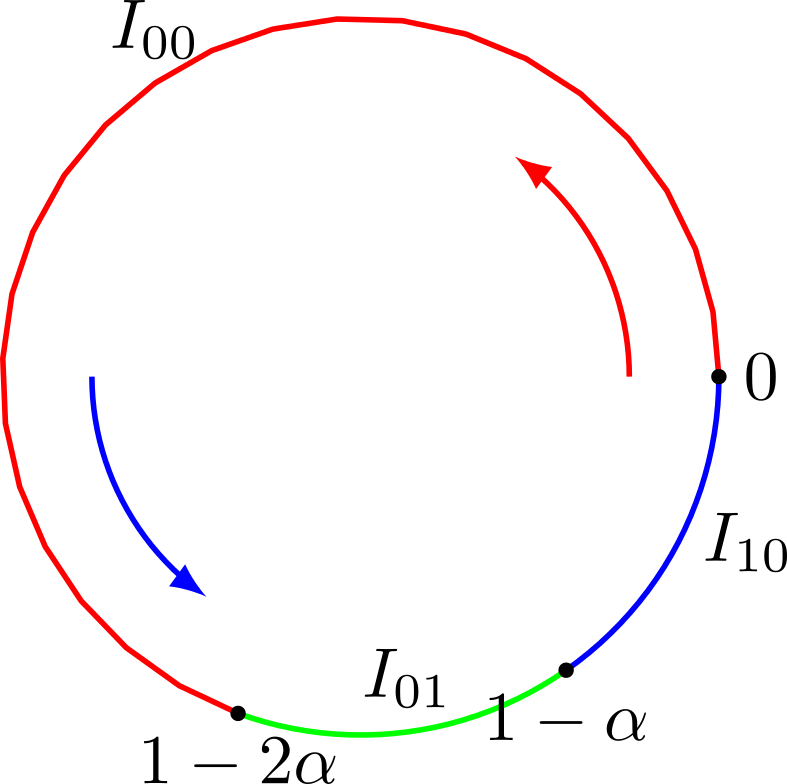
Remark [Complexity of a Sturmian word] Since $\alpha$ is irrational, the points

$$0,-\alpha,-2\alpha,\ldots,-m\alpha\,,$$

modulo $1$ are all distinct.

Thus the the above points delimit $m+1$ circle intervals: we have $m+1$ factors $w\in {0,1}^m$ of length $m$ appearing in $\bf{u}$. This is the smallest possible number of factors of length $m$ in the sense that, if we had at most $m$ factors of length $m$ for some $m$, our words would be eventually periodic.

The intervals-factor correspondence is independent from $\beta$. In particular, the set of factors of length $m$ appearing within ${\bf{u}}$ depends only on the choice of $\alpha$. Furthermore, the sequence ${n\alpha}$ is equidistributed (also known as uniform distribution $\bmod. 1$) meaning that the proportion of the time it spends on an interval $I$ tends to its length $\left| I \right|$. Thus the initial point $y_0=\beta$ is not really important for our purposes.

The smallest (least frequent) interval delimited by

$$0,-\alpha,-2\alpha,\ldots,-m\alpha\,,$$

in fact corresponds to the one given by $0$ and $\{-q_k\alpha\}$, where $q_k(\alpha)\leq m < q_{k+1}(\alpha)$, and has length $\Gamma(\alpha,m) := |q_k \alpha - p_k|$, by the Theorem of the Best approximation section in the previous post.